Uso de relaciones
El concepto de relación implica la idea de enumeración, de algunos de los elementos, de los conjuntos que forman tuplas.
Aplicaciones numéricas, recuperación de información y problemas de redes son algunos ejemplos donde
Las relaciones ocurren como parte de la descripción del problema, y la manipulación de relaciones es
Importante en la resolución de procedimientos.
Las relaciones también juegan un importante papel en la teoría de computación, incluyendo estructuras de programas y análisis de algoritmos.
Producto cartesiano
Considere dos conjuntos arbitrarios A y B. El conjunto de todas las parejas ordenadas (a, b) en
donde a ∈ A y b ∈ B se llama producto o producto cartesiano de A y B.La definición de producto cartesiano puede extenderse fácilmente al caso de más de dosconjuntos.Se llama producto cartesiano de dos conjuntos A y B y se representa A x B, al conjunto depares ordenados (a, b), tales que el primer elemento pertenece al primer conjunto y el segundoelemento al segundo conjunto. Es decir:A x B = {(a, b) / a ∈ A, b ∈ B}
El producto cartesiano, en general, no es conmutativo. Es decir: A x B ≠ B x A.Puede ocurrir que los conjuntos A y B sean coincidentes.EJEMPLO:
Si A = {a, b, c} y B = {1, 2, 3, 4}, el producto cartesiano es:A x B = {(a, 1), (a, 2), (a, 3), (a, 4), (b, 1), (b, 2), (b, 3), (b, 4), (c, 1), (c, 2), (c, 3), (c, 4)}Se puede representar gráficamente por medio de puntos en un plano, como se muestra acontinuación. Aquí, cada punto P representa una pareja ordenada (a, b) de números reales yviceversa; la línea vertical a través de P encuentra al eje x en a, y la línea horizontal a través de Pencuentra el eje y en b. A esta representación se le conoce como diagrama cartesiano.
Relaciones binarias
es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados.
Una relación (binaria) R de un conjunto X a un conjunto Y es un subconjunto del producto cartesiano X × Y. si (x, y) ? R escribimos xRy y decimos que x esta relacionado con y.
Una relación que es reflexiva, simétrica y transitiva en un conjunto X se llama relación de equivalencia sobre X.
Ejemplos:
a) Sean los conjuntos X = {a, b, c, d} y Y = {1, 2, 3, 4}, definir una relación R de X en Y y determinar el dominio de R y lel rango de R.
R = {(a, 1), (b, 2), (c, 3), (d, 4)}
El dominio se define por el conjunto {x ? X/(x, y) ? R para algún y ? Y}
dominio de R es el conjunto {a, b, c, d}
b) La relación R sobre X = {1, 2, 3, 4} esta definida por “(x, y) ? R si x = y“ es:
R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}
el dominio de R es el conjunto {1, 2, 3, 4}
el rango de R es el conjunto {1, 2, 3, 4}
se concluye que: el dominio y el rango son iguales porque la relación está definida sobre el mismo conjunto X.
La digráfica de la relación R es la siguiente:
Matriz de una relación
Grafo de una relación
a) Un GRAFO NO DIRIGIDO G consiste en un conjunto V de vértices (o nodos) y un conjunto E de aristas (o arcos) tal que cada arista e ? E se asocia con un par no ordenado de vértices. Entonces se puede decir que si existe una arista e entre un par de vértices v y w, esta puede ser igual a: e = ( v, w) o e = ( w, v)
Los vértices del grafo G son: V_1, V_2, V_3, V_4 entonces V = {V_1, V_2, V_3, V_4}
Las aristas del grafo son: e_1, e_2, e_3, e_4 entonces E = {e_1, e_2, e_3, e_4}
Entonces podemos decir que G = {{V_1, V_2, V_3, V_4}, {e_1, e_2, e_3, e_4}}
Como el grafo G no tiene lazos ni lados paralelos entonces es un grafo simple.
Otro ejemplo de grafo no dirigido es el siguiente:
Clasificación por tipos de relaciones
Una relación tiene la propiedad reflexiva, si todo elemento esta relacionado consigo mismo, si no todos los elementos del conjunto están relacionados consigo mismo se dice que la relación no es reflexiva.
R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}se dice que es reflexiva por que cada elemento x ? X, (x, x) ? R; los pares ordenados (1, 1), (2, 2), (3, 3) y (4, 4) están en R. Si observamos la digráfica de la relación reflexiva, encontramos que tiene un lazo sobre cada vértice.
Para todo elemento a que pertenezca al conjunto A, el par ordenado (a,a) pertenece a la relación binaria R.
Téngase en cuenta que debe cumplirse para todos los elementos del conjunto sin excepción, si esta propiedad solo se da en algunos casos la relación no es reflexiva:
No existe ningún elemento a en A, para el que el par ordenado (a,a) no pertenezca a la relación R. Puede verse que estas dos afirmaciones son iguales.
Irreflexiva
Una relación binaria tiene la propiedad irreflexiva, también llamada: antirreflexiva o antirrefleja, si ningún elemento del conjunto esta relacionado consigo mismo:
Que también puede expresarse
No existe ningún elemento a en el conjunto A que cumpla que: (a,a) pertenezca a R.
Simétrica
Una relación binaria tiene la propiedad simétrica, si se cumple que un par ordenado (a,b) pertenece a la relación entonces el par (b,a) también pertenece a esa relación:
R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}
“no es simétrica”, por cuanto no cumple la definición que dice: “si para cada x, y ? X, si (x, y) ? R, entonces (y, x) ? R”.
Para todo par ordenado (a,b) que pertenezca a R, implica que el par (b,a) también pertenece a R, téngase en cuenta que si el par (a,b) no pertenece a la relación el par (b,a)tampoco tiene que pertenecer a esa relación:
No existe ningún par ordenado (a,b) que pertenezca a R y que el par (b,a) no pertenezca a R.
Antisimétrica
Una relación binaria se dice que tiene la propiedad antisimétrica si los pares ordenado (a,b) y (b,a) pertenecen a la relación entonces a = b:
R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}
“la relación R sobre el cojunto X es antisimétrica”, por cuanto cumple la definición que dice para toda: “x, y X, si (x, y) ? R y x ? y, entonces (x, y) ? R”. Específicamente tenemos (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4) pertenecen a R, pero (2, 1), (3, 1), (4, 1), (3, 2), (4, 2), (4, 3) no pertenecen a R.
Dicho de otra manera, no existen los elementos a, b distintos, y que a este relacionado con b y b este relacionado con a
Una relación binaria tiene la propiedad transitiva cuando, dado los elementos a, b, c del conjunto, si a esta relacionado con b y b esta relacionado con c, entonces a esta relacionado con c:
R = {(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4), (3, 3), (3, 4), (4, 4)}
“es una relación transitiva R sobre el cojunto X”, por cuanto cumple la definición que dice: “x, y, z ? X, si (x, y) y (y, z) ? R, entonces (x, z) ? R”.
Específicamente tenemos (1, 2), (2, 3) se tiene (1, 3); (1, 3), (3, 4) se tiene (1, 4); (2, 3), (3, 4) se tiene (2, 4) todos pertenecen a R.
Relaciones de equivalencia, clases de equivalencia y particiones
de clase de equivalencia:
![[a] = \{b\in K\,|\,b\mathcal{R}a\}](https://upload.wikimedia.org/math/b/2/0/b20415fb5ae7f86ec49868218a52bc3f.png)
La relación de equivalencia  define subconjuntos disjuntos en
define subconjuntos disjuntos en  llamados clases de equivalencia:
llamados clases de equivalencia:
 define subconjuntos disjuntos en
define subconjuntos disjuntos en  llamados clases de equivalencia:
llamados clases de equivalencia:
Dado un elemento 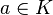 , el conjunto dado por todos los elementos relacionados con
, el conjunto dado por todos los elementos relacionados con  definen la clase:
definen la clase:
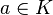 , el conjunto dado por todos los elementos relacionados con
, el conjunto dado por todos los elementos relacionados con  definen la clase:
definen la clase:
se le llama la clase de equivalencia asociada al elemento  .
.
 .
.
Al elemento  se le llama representante de la clase.
se le llama representante de la clase.
 se le llama representante de la clase.
se le llama representante de la clase.
Se llama orden al número de clases que genera una relación de equivalencia; si éste es finito, se dice que la relación es de orden finito.
El concepto de clase de equivalencia tiene importancia en ciencia, dado un conjunto de objetos o entidades abstractas (potencialmente infinitas), pueden establecerse relaciones de equivalencia en base a algún criterio, las clases resultantes son los "tipos" en los que se puede clasificar toda la gama de objetos.
Operaciones entre relaciones
Complemento de R
Puede definirse el complemento de una relación como el como el conjunto de todos los pares ordenados del producto cartesiano AB que no estan en , y se representa como ó ~.
Ejemplo:
Sean y dos relaciones de X a Y y de U a V respectivamente. Además tenemos que
Dom()={a, b, c} Cod()={A, B, C}, Dom()={a,b} Cod()={B,C} y sean
={(a, A), (a, B), (b, C)} y ={(a, B), (b, C)}
Entonces XY={(a, A), (a, B), (a, C), (b, A), (b, B), (b, C), (c, A), (c, B), (c, C)}
Por lo tanto ={(a, c), (b, A), (b, B), (c, A), (c, B), (c, C)}
Y para UV ={(a, B), (a, C), (b, B), (b, C)}
se tiene que ={(a, C), (b, B)}.
El complemento de r de un número positivo N en base r con una parte entera de n dígitos, será definido como el complemento de r a n y se define como rn-N;
El complemento de 10 de un número decimal se puede formar dejando todos los ceros significativos sin cambios se resta el primer dígito del cero menos significativo de 10 y, entonces se restan todos los pocos dígitos menos significativos menores de 9.
Ejemplo:
Obtener el complemento de 10 de (52520)10
105-52520=47480
El complemento de 2 puede formarse dejando todos los ceros menos significativos y el primer dígito diferente de 0 sin cambio, entonces se reemplazan los 1 por 0 y los 0 por 1 en los otros dígitos mas significativos.
Ejemplo :
Obtener el complemento de 2 de (101100)2
26-(101100)2 = (100000)2-(101100)2=(0.1010)2
Intersección
Dos conjuntos son ajenos o disjuntos cuando su intersección es el conjunto vacío, es decir, que no tienen nada en común. Por ejemplo:
Unión

Un grafo, G, es un par ordenado de V y A, donde V es el conjunto de vértices o nodos del grafo y A es un conjunto de pares de vértices, a estos también se les llama arcos o ejes del grafo. Un vértice puede tener 0 o más aristas, pero toda arista debe unir exactamente a dos vértices.Los grafos representan conjuntos de objetos que no tienen restricción de relación entre ellos. Un grafo puede representar varias cosas de la realidad cotidiana, tales como mapas de carreteras, vías férreas, circuitos eléctricos, etc.La notación G = A (V, A) se utiliza comúnmente para identificar un grafo.Los grafos se constituyen principalmente de dos partes: las aristas, vértices y los caminos que pueda contener el mismo grafo.
Un grafo (G) es un diagrama que consta de un conjunto de nodos (Vértices) y un conjunto de aristas (lados).
Nodos. Se indican por medio de un pequeño circulo y se le asigna un numero o una letra.
Aristas. Son las lineas que unen un nodo con otro y se les asigna una letra un numero o una combinación de ambos.
Aristas paralelas. Son las aristas que tienen relación con un mismo par de nodos.
Lazo. Es aquella arista que sale de un nodo y regresa al mismo nodo.
Valencia de un nodo. Es el numero de aristas que salen o entran a un nodo.
Grafo regular: Aquel con el mismo grado en todos los vértices. Si ese grado es k lo llamaremos k-regular.
Grafo bipartito: Es aquel con cuyos vértices pueden formarse dos conjuntos disjuntos de modo que no haya adyacencias entre vértices pertenecientes al mismo conjunto
Grafo completo: Aquel con una arista entre cada par de vértices. Un grafo completo con n vértices se denota Kn.
Grafo bipartito regular: se denota Km,n donde m, n es el grado de cada conjunto disjunto de vértices.
Grafo nulo: Se dice que un grafo es nulo cuando los vértices que lo componen no están conectados, esto es, que son vértices aislados.
Grafos Isomorfos: Dos grafos son isomorfos cuando existe una correspondencia biunívoca (uno a uno), entre sus vértices de tal forma que dos de estos quedan unidos por una arista en común.
Grafos Platónicos: Son los Grafos formados por los vértices y aristas de los cinco sólidos regulares (Sólidos Platónicos), a saber, el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro.




El primer renglón nos dará el número complejo. Podemos definir la unidad real como
y la imaginaria como
al ser un número complejo la suma de un número real más otro número real por la unidad imaginaria, podemos hacerlo matricialmene
Un grafo o multigrafo que se puede dibujar en el plano sin que se crucen sus arcos se llama plano. Aunque el grafo completo de K4 se suele dibujar con arcos que se cruzan como en la figura 6.1(a), también se puede dibujar sin que se crucen sus arcos como en la figura 6.1(b). Luego K4 es un grafo plano.

En este contexto árboles y grafos se refiere a estructuras de datos que permiten organizar y mantener información en un computador. Esta forma se inspira una forma de organizar información con lápiz y papel usando nodos y flechas entre los nodos (a esas flechas también se les llama arcos, a los nodos también se les llama vértices). Los grafos y árboles en papel son apropiados por ejemplo para capturar sólo una parte de la información de objetos, situaciones y otros tipos de información
La unión de los conjuntos A y B es el conjunto de todos los elementos de A con todos los elementos de B sin repetir ninguno y se denota como A∪ B . Esto es:
El conjunto inverso es otra denominación del conjunto complementario, es decir, el conjunto inverso de A es el conjunto de los elementos del universal que no están en A.
Si el universal U son las vocales, U={a, e, i, o, u} y A = {a, e, o} el inverso de A = {i, u}
Conjunto vacío es un conjunto sin elementos.
Conjunto infinito es el que tiene el mismo número de elementos que algún subconjunto propio suyo. Por ejemplo el número de números naturales, N={1, 2, 3, 4, ....} y el de pares 2N = {2, 4, 6, 8,..} es el mismo (basta escribir uno bajo otro: hay el mismo número de elementos en ambas filas):
1, 2, 3, 4, ....
2, 4, 6, 8, ...
Luego los números naturales tienen el mismo número de elementos que los pares, que son un subconjunto propio de él, luego los naturales son un conjunto infinito.
Esta definición implica que (x, ) está en la composición de las relaciones hermana y padre, si existe un individuo y tal que x es hermana de y e y es un padre de z. Esto es exactamente la relación tía. De esto se sigue, que la relación tía es la composición de la relación hermana y padre como hemos afirmado. En general, para determinar si (x, z) está en la relación R o S, se necesita siempre un intermediario y la hermana, en el caso de la relación tía, tal que sean válidas xRy e yRz.
Empleo de grafos
Un grafo (G) es un diagrama que consta de un conjunto de nodos (Vértices) y un conjunto de aristas (lados).
Nodos. Se indican por medio de un pequeño circulo y se le asigna un numero o una letra.
Aristas. Son las lineas que unen un nodo con otro y se les asigna una letra un numero o una combinación de ambos.
Aristas paralelas. Son las aristas que tienen relación con un mismo par de nodos.
Lazo. Es aquella arista que sale de un nodo y regresa al mismo nodo.
Valencia de un nodo. Es el numero de aristas que salen o entran a un nodo.
Tipos de grafos
Por ejemplo, el primero de los siguientes grafos es 3-regular, el segundo es 2-regular y el tercero no es regular.
Ejemplo.- de los dos grafos siguientes el primero es bipartito y el segundo no lo es.
Representación matricial
Un número complejo se puede representar como un vector y un vector como matriz,por lo que suena lógico que un número complejo se pueda representar con una matriz, sólo que la representación no tiene que ser propiamente la de un vector en una matriz. Una posible representación de  con
con  y
y 
Con esta representación la aritmetica compleja es isomorfa a las operaciones con matrices.
Caminos y circuitos
Camino.
Es una sucesión de lados que van de un nodo x a un nodo w (dichos lados se pueden repetir).
Circuito o ciclo.
Es un camino del nodo w al nodo w, esto es, un camino que regresa al mismo nodo de donde salió.
Circuito simple de longitud n.
Es aquel camino del nodo w al nodo w que solamente tiene un ciclo en la ruta que sigue.
Camino simple de longitud n.
Es una sucesión de lados que van de un nodo x a un nodo w, en donde los lados que componen dicho camino son distintos e iguales a n. Esto significa que no se puede pasar dos veces por una misma arista.
Camino de Euler.
Es aquel camino que recorre todos los nodos pasando por todas las aristas solamente una vez. Una característica importante de los grafos que tienen camino de Euler es que siempre comienzan y terminan en nodos que terminan en valencia impar.
Circuito de Euler.
Es aquel ciclo que recorre todos los nodos pasando por todos las aristas solamente una vez.
Un grafo tiene un Circuito de Euler si y solo si es conexo y todos sus nodos tienen valencia par.
Isomorfismo
El concepto matemático de isomorfismo pretende captar la idea de tener la misma estructura
Dos estructuras matemáticas entre las que existe una relación de isomorfismo se llaman isomorfas.
Grafos planos
Uso de arboles
Los árboles son una clase de grafos. Un claro ejemplo de un árbol es el siguiente:
Consideremos cuatro parejas de chismosos {a, A, b, B, c, C, d, D} donde a, b, c y d son los esposos y A, B, C y D son sus esposas respectivamente. Supongamos que a llama a su esposa para contarle algún chisme, entonces ella llama a las otras señoras para difundir el chisme, y cada una de ellas a su vez llama a su esposo para comunicárselo. El siguiente grafo muestra la propagación del chisme:
Un árbol es un grafo no dirigido conexo que no contiene circuitos, es decir que no existen dos o más paseos sobre un par de vértices.
Un conjunto de árboles disjuntos es llamado bosque. Un vértice de grado 1 en un árbol se llama hoja o un nodo terminal, y un vértice de grado mayor que 1 recibe el nombre de rama o nodo interno. Por ejemplo, son hojas: b, c, d y los vértices a, A, B, C, D son nodos rama.
Propiedades de los arboles
Las propiedades de los árboles son:
• Existe un único paseo entre dos vértices cualesquiera de un árbol.
• El número de vértices es mayor en uno al número de aristas de un árbol.
• Un árbol con dos o más vértices tiene al menos dos hojas.
Un árbol T (libre) es una gráfica simple que satisface lo siguiente; si v y w son vértices en T, existe una trayectoria simple única de v a w.
En este contexto árboles y grafos se refiere a estructuras de datos que permiten organizar y mantener información en un computador. Esta forma se inspira una forma de organizar información con lápiz y papel usando nodos y flechas entre los nodos (a esas flechas también se les llama arcos, a los nodos también se les llama vértices). Los grafos y árboles en papel son apropiados por ejemplo para capturar sólo una parte de la información de objetos, situaciones y otros tipos de información


